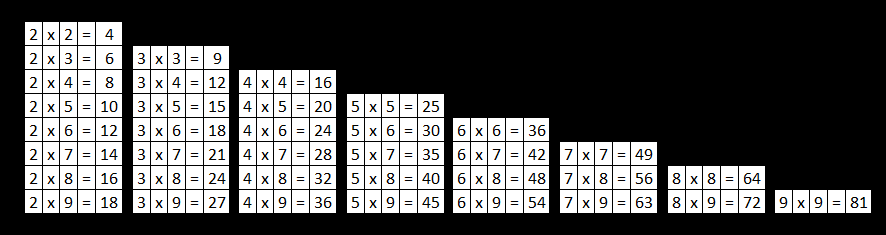
Finding Square Roots in the traditional way, i.e. by long division method is quite time-consuming.

However, there is a much simpler and faster method of finding square roots of a perfect square. In Vedic Maths, we use Sutra “The First by the First and the Last by the Last“.

A perfect square is an integer that is the square of another integer. For example, 1024 is a perfect square of 32. Here, 1024 and 32 both are integers.

Square of 32 or 32 ^2 = 1024.

So, the square root of 1024 or √1024 is 32.

Let’s understand the method to find square root of any perfect square with this example.

√1024 = 32

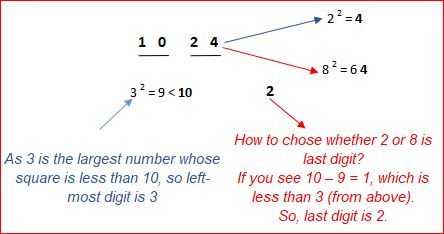
Step 1: We have to mark the digits in the number in pairs starting from the right, i.e. 24 as one pair, 10 as another pair in 1024.

The leftmost pair gives the left-most digit of the answer.

The rightmost pair give the right-most digit of the answer.

Step 2: Find the leftmost part of the answer.

Consider the leftmost pair first, i.e. 10 in this case is the leftmost pair.

The largest number whose square is less than 10 is 3 (3^2 = 9).

So, the leftmost digit of the answer is 3.

 Step 3: Find the rightmost part of the answer.

Consider the rightmost pair, i.e. 24 in this case is the rightmost pair.

Since the number 1024 ends in 4, so the last digit in the answer will be either 2 or 8 (as only square of 2 (= 4) or square of (8 = 64) ends in 4).

How to chose whether 2 or 8 is the last digit?

From Step 2, find the remainder of 10 – 9 (= 1). As 1 is less than 3 (obtained from step 2), the last digit will be 2.

Had the above remainder been greater than 3, then the last digit would have been 8.

Let’s understand this from below graphical representation:

Take another example:

√2209 = 47